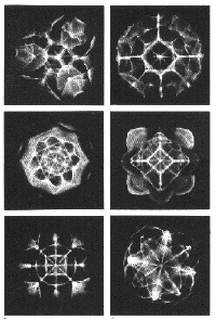
CYMATICS : Sound of Creation
"Since all things are made by the power of sound, of vibration, so can man create his world by the same power.
The knowledge of sound is supreme for it is beyond all form. By the knowledge of sound we obtain the knowledge
of creation and the mastery of that knowledge helps us to rise to the formless. This knowledge acts as our wings,
helping us to rise from earth to heaven and penetrate through life seen and unseen."
(Hazrat Jnayat Khan)
The knowledge of sound is supreme for it is beyond all form. By the knowledge of sound we obtain the knowledge
of creation and the mastery of that knowledge helps us to rise to the formless. This knowledge acts as our wings,
helping us to rise from earth to heaven and penetrate through life seen and unseen."
(Hazrat Jnayat Khan)
|
_The Miracle of 528 Hz Solfeggio
and Fibonacci numbers
|
Cymatics : The Science of the Future?
Evan Grant: Making sound visible through Cymatics
Evan Grant demonstrates the science and art of cymatics, a process for making soundwaves visible. Useful for analyzing complex sounds (like dolphin calls), it also makes complex and beautiful designs. 
Is there a connection between sound, vibrations and physical reality? Do
sound and vibrations have the potential to create?
In this article we will see what various researchers in this field, which has been given the name of Cymatics, have concluded. By Peter Pettersson, translation Yarrow Cleaves In 1787, the jurist,
musician and physicist Ernst Chladni published ‘Entdeckungen über die Theorie des Klangesor Discoveries’ - ’Concerning the Theory of Music’. In
this and other pioneering works, Chladni, who was born in 1756, the same year
as Mozart, and died in 1829, the same year as Beethoven, laid the foundations
for that discipline within physics that came to be called acoustics, the
science of sound.
Among Chladni’s successes was finding a way to make visible what sound waves generate. With the help of a violin bow, which he drew perpendicularly across the edge of flat plates covered with sand, he produced those patterns and shapes which today go by the term ‘Chladni figures’. What was the significance of this discovery? Chladni demonstrated once and for all that sound actually does affect physical matter and that it has the quality of creating geometric patterns. Chladni figures
What
we are seeing in this illustration is primarily two things: areas that are and
are not vibrating. When a flat plate of an elastic material is vibrated, the
plate oscillates not only as a whole but also as parts. The boundaries between
these vibrating parts, which are specific for every particular case, are called
node lines and do not vibrate. The other parts are oscillating constantly.
If sand is then put on this vibrating plate, the sand (black in the illustration) collects on the non-vibrating node lines. The oscillating parts or areas thus become empty. According to Dr Hans Jenny, the converse is true for liquids; that is to say, water lies on the vibrating parts and not on the node lines. Lissajous Figures In 1815 the American mathematician Nathaniel Bowditch began studying the patterns created by the intersection of two sine curves whose axes are perpendicular to each other, sometimes called Bowditch curves but more often ‘Lissajous figures’, after the French mathematician Jules-Antoine Lissajous who, independently of Bowditch, investigated them in 1857-58. Both concluded that the condition for these designs to arise was that the frequencies, or oscillations per second, of both curves stood in simple whole-number ratios to each other, such as 1:1, 1:2, 1:3, and so on. In fact, one can produce Lissajous figures even if the frequencies are not in perfect whole-number ratios to each other. If the difference is insignificant, the phenomenon that arises is that the designs keep changing their appearance. They move. What creates the variations in the shapes of these designs is the phase differential, or the angle between the two curves. In other words, the way in which their rhythms or periods coincide. If, on the other hand, the curves have different frequencies and are out of phase with each other, intricate web-like designs arise. These Lissajous figures are all visual examples of waves that meet each other at right angles. Lissajous figures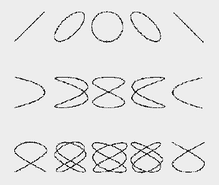
The result of two sine curves meeting at right angles.
Illustration: Typoform, Jenny W. Bryant, Swedish National Encyclopaedia As I pondered the connection between these figures and other areas of knowledge, I came to think about the concept that exists in many societies and their mythologies around the world, which describes the world as a web. For example, many of the Mesoamerican people regarded the various parts of the universe as products of spinning and weaving: "Conception and birth were/.../ compared with the acts of spinning and weaving; all the Aztec and Mayan creation and fertility goddesses were described as great weavers". A number of waves crossing each other at right angles look like a woven pattern, and it is precisely that they meet at 90-degree angles that gives rise to Lissajous figures. Dr Hans Jenny (Dr Jenny's work is demonstrated in the three YouTube videos in the left column) In 1967, the late Hans Jenny, a Swiss doctor, artist, and researcher, published the bilingual book ‘Kymatik -Wellen und Schwingungen mit ihrer Struktur und Dynamik/ Cymatics’ – ‘The Structure and Dynamics of Waves and Vibrations’. In this book Jenny, like Chladni two hundred years earlier, showed what happens when one takes various materials like sand, spores, iron filings, water, and viscous substances, and places them on vibrating metal plates and membranes. What then appears are shapes and motion-patterns which vary from the nearly perfectly ordered and stationary to those that are turbulently developing, organic, and constantly in motion. Dr Hans Jenny

Jenny made use of crystal oscillators and an invention of his own by the
name of the tonoscope to set these plates and membranes vibrating. This was a
major step forward. The advantage with crystal oscillators is that one can
determine exactly which frequency and amplitude/volume one wants. It was now
possible to research and follow a continuous train of events in which one had
the possibility of changing the frequency or the amplitude or both.
The tonoscope was constructed to make the human voice visible without any electronic apparatus as an intermediate link. This yielded the amazing possibility of being able to see the physical image of the vowel, tone or song a human being produced directly. Not only could you hear a melody - you could see it, too! Jenny called this new area of research ‘Cymatics’, which comes from the Greek kyma, wave. Cymatics could be translated as: the study of how vibrations, in the broad sense, generate and influence patterns, shapes and moving processes. The Creative Vibration What did Hans Jenny find in his investigations? In the first place, Jenny produced both the Chladni figures and Lissajous figures in his experiments. He discovered also that if he vibrated a plate at a specific frequency and amplitude - vibration - the shapes and motion patterns characteristic of that vibration appeared in the material on the plate. If he changed the frequency or amplitude, the development and pattern were changed as well. He found that if he increased the frequency, the complexity of the patterns increased, the number of elements became greater. If on the other hand he increased the amplitude, the motions became all the more rapid and turbulent and could even create small eruptions, where the actual material was thrown up in the air. 
Sand patterns as a function of the size of the plate
The shapes, figures and patterns of motion that appeared proved to be primarily a function of frequency, amplitude, and the inherent characteristics of the various materials. He also discovered that under certain conditions he could make the shapes change continuously, despite his having altered neither frequency nor amplitude! 
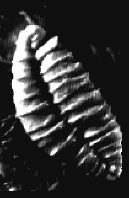
The vowel ‘A’ in sand
When Jenny experimented with fluids of various kinds he produced wave motions, spirals, and wave-like patterns in continuous circulation. In his research with plant spores, he found an enormous variety and complexity, but even so, there was a unity in the shapes and dynamic developments that arose. With the help of iron filings, mercury, viscous liquids, plastic-like substances and gases, he investigated the three-dimensional aspects of the effect of vibration. In his research with the tonoscope, Jenny noticed that when the vowels of the ancient languages of Hebrew and Sanskrit were pronounced, the sand took the shape of the written symbols for these vowels, while our modern languages, on the other hand, did not generate the same result! How is this possible? Did the ancient Hebrews and Indians know this? Is there something to the concept of "sacred language", which both of these are sometimes called? What qualities do these "sacred languages", among which Tibetan, Egyptian and Chinese are often numbered, possess? Do they have the power to influence and transform physical reality, to create things through their inherent power or, to take a concrete example, through the recitation or singing of sacred texts, to heal a person who has gone "out of tune"? 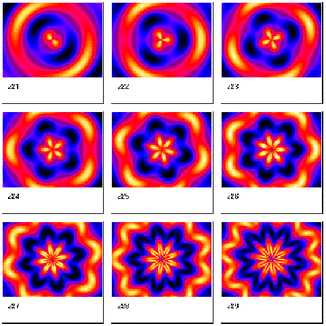
Sound structures in the water drop as a function of the wavelength
An interesting phenomenon appeared when he took a vibrating plate covered with liquid and tilted it. The liquid did not yield to gravitational influence and run off the vibrating plate but stayed on and went on constructing new shapes as though nothing had happened. If, however, the oscillation was then turned off, the liquid began to run, but if he was really fast and got the vibrations going again, he could get the liquid back in place on the plate. According to Jenny, this was an example of an anti-gravitational effect created by vibrations. Universality? At the beginning of ‘Cymatics’, Hans Jenny says the following: "In the living as well as non-living parts of nature, the trained eye encounters wide-spread evidence of periodic systems. These systems point to a continuous transformation from the one set condition to the opposite set". Jenny is saying that we see everywhere examples of vibrations, oscillations, pulses, wave motions, pendulum motions, rhythmic courses of events, serial sequences, and their effects and actions. Throughout the book Jenny emphasises his conception that these phenomena and processes not be taken merely as subjects for mental analysis and theorizing. Only by trying to "enter into” phenomena through empirical and systematic investigation can we create mental structures capable of casting light on ultimate reality. He asks that we not "mix ourselves in with the phenomenon" but rather pay attention to it and allow it to lead us to the inherent and essential. He means that even the purest philosophical theory is nevertheless incapable of grasping the true existence and reality of it in full measure. 
What Hans Jenny pointed out is the resemblance between the shapes and
patterns we see around us in physical reality and the shapes and patterns he
generated in his investigations. Jenny was convinced that biological evolution
was a result of vibrations, and that their nature determined the ultimate
outcome. He speculated that every cell had its own frequency and that a number
of cells with the same frequency created a new frequency which was in harmony
with the original, which in its turn possibly formed an organ that also created
a new frequency in harmony with the two preceding ones.
Trinity In the closing chapter of the book ‘Cymatics’, Jenny sums up these phenomena in a three-part unity. The fundamental and generative power is in the vibration which, with its periodicity, sustains phenomena with its two poles. At one pole we have form, the figurative pattern. At the other is motion, the dynamic process. These three fields - vibration and periodicity as the ground field, and form and motion as the two poles - constitute an indivisible whole, Jenny says, even though one can dominate sometimes. Does this trinity have something within science that corresponds? Yes, according to John Beaulieu, American polarity and music therapist. In his book ‘Music and Sound in the Healing Arts’, he draws a comparison between his own three-part structure, which in many respects resembles Jenny’s, and the conclusions researchers working with subatomic particles have reached. "There is a similarity between cymatic pictures and quantum particles. In both cases that which appears to be a solid form is also a wave. They are both created and simultaneously organized by the principle of pulse (Read: principle of vibration). This is the great mystery with sound: there is no solidity! A form that appears solid is actually created by an underlying vibration". In an attempt to explain the unity in this dualism between wave and form, physics developed the quantum field theory, in which the quantum field or, in our terminology, the vibration, is understood as the one true reality, and the particle or form, and the wave or motion, are only two polar manifestations of the one reality, vibration, says Beaulieu. In conclusion, I would like to cite Cathie E. Guzetta’s poetic contemplation of where the investigation of the relationship between sound and the arising of various life forms might lead us in the future: "The forms of snowflakes and faces of flowers may take on their shape because they are responding to some sound in nature. Likewise, it is possible that crystals, plants, and human beings may be, in some way, music that has taken on visible form." Disclaimer: The quotes from Hans Jenny’s book ‘Cymatics’ are not exactly as they appear in the book, although the overall spirit and meaning of the quotes are accurate. http://www.world-mysteries.com/sci_cymatics.htm |